Plain concrete beams are inefficient as flexural members because the tensile strength in bending (modulus of rupture) is a small fraction of the compressive strength. As a consequence, such beams fail on the tension side at low loads long before the strength of the concrete on the compression side has been fully utilized. For this reason, steel reinforcing bars are placed on the tension side as close to the extreme tension fiber as is compatible with proper fire and corrosion protection of the steel. In such a reinforced concrete beam, the tension caused by the bending moments is chiefly resisted by the steel reinforcement, while the concrete alone is usually capable of resisting the corresponding compression. Such joint action of the two materials is assured if relative slip is prevented. This is achieved by using deformed bars with their high bond strength at the steel-concrete interface and, if necessary, by special anchorage of the ends of the bars. A simple example of such a beam, with the customary designations for the cross-sectional dimensions, is shown in figure below. For simplicity, the discussion that follows will deal with beams of rectangular cross section, even though members of other shapes are very common in most concrete structures.
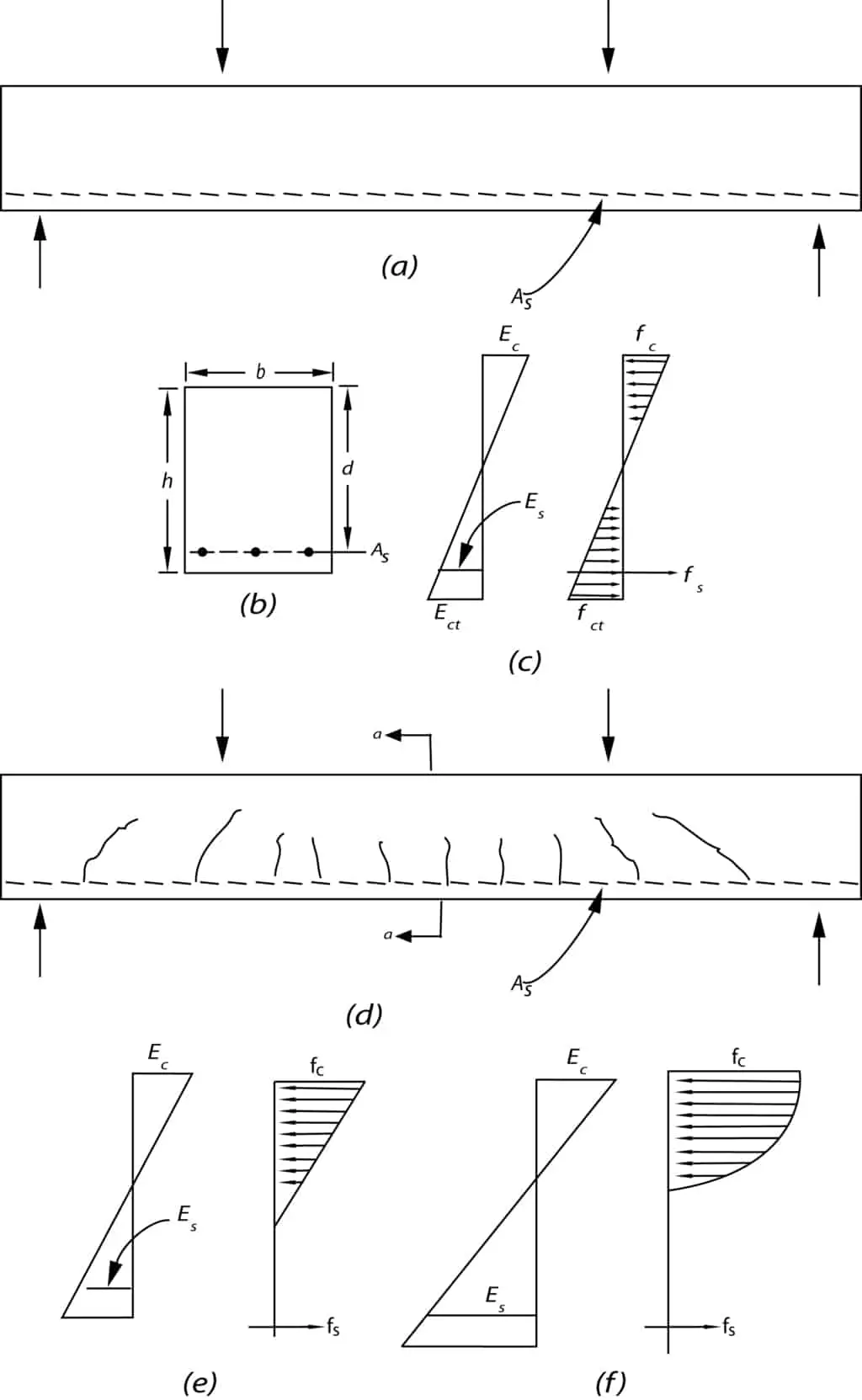
When the load on such a beam is gradually increased from zero to the magnitude that will cause the beam to fail, several different stages of behavior can be clearly distinguished. At low loads, as long as the maximum tensile stress in the concrete is smaller than the modulus of rupture, the entire concrete is effective in resisting stress, in compression on one side and in tension on the other side of the natural axis. In addition, the reinforcement, deforming the same amount as the concrete, is also subject to tensile stresses. At this stage, all stresses in the concrete are of small magnitude and are proportional to strains. The distribution of strains and stresses in concrete and steel over the dept of the section is as shown in fig c.
When the load is further increased, the tensile strength of the concrete is soon reached, and at this stage tension cracks develop. These propagate quickly upward to or close to the level of the natural plane, which in turn shifts upward with progressive cracking. The general shape and distribution of these tension cracks is shown in fig d. In well-designed beams, the width of these cracks is so small (hairline cracks) that they are not objectionable from the viewpoint of either corrosion protection or appearance. Their presence, however, profoundly affects the behavior of the beam under load. Evidently, in a cracked section, i.e., in a cross section located at a crack such as a-a in fig. d, the concrete does not transmit any tensile stress. Hence, just as in tension members, the steel is called upon to resist the entire tension. At moderate loads, if the concrete stress do not exceed approximately— fc1/2—- stresses and strains continue to be closely proportional. The distribution of strains and stresses at or near a cracked section is than thet shown in fig e. when the load is still further increased; stresses and strains rise correspondingly and are no longer proportional. The ensuing nonlinear relation between stresses and strains is that given by the concrete stress-strain curve. Therefore, just as in homogeneous beams, The distribution of concrete stresses on the compression side of the beam is of the same shape as the stress-strain curve. Figure f shows the distribution of strains and stresses close to the ultimate load.
Eventually, the carrying capacity of the beam is reached. Failure can be caused in one of two ways. When relatively moderate amounts of reinforcement are employed, at some value of the load and steel will reach its yield point. At that stress, the reinforcement yields suddenly and stretches a large amount, and the tension cracks in the concrete widen visibly propagate upward, with simultaneous significant deflation of the beam. When this happens, the strains in the remaining compression zone of the concrete increase to such degree that crushing of the concrete , The secondary compression failure, ensues at a load only slightly large than that which caused the steel to yield. Effectively, therefore, attainment of the yield point in the steel determines the carrying capacity of moderately reinforced beams. Such yield failure is gradual and is preceded by visible signs of distress, such as the widening and lengthening of cracks and the marked increase in deflection.
On the other hand, if large amounts of reinforcement or normal amounts of steel of very high strength are employed, the compressive strength of the concrete may be exhausted before the steel starts yielding. Concrete fails by crushing when strains become so large that they disrupt the integrity of the concrete. Exact criteria for this occurrence are not yet known, but is has been observed that rectangular beams ail in compression when the concrete strains reach values of about 0.003 to 0.004. Compression failure through crushing of the concrete is sudden, of an almost explosive nature, and occurs without warning. For this reason it is good practice to dimension beams in such a manner that should they be overloaded, failure would be initiated by yielding of the steel rather then by crushing of the concrete. (Source: Nelson)
