Beams must have an adequate safety margin against other types of failure, some of which may be more dangerous than flexural failure. This may be so because of greater uncertainly in predicting certain other modes of collapse, or because of the catastrophic nature of some other types of failure, should they occur.
Shear Failure
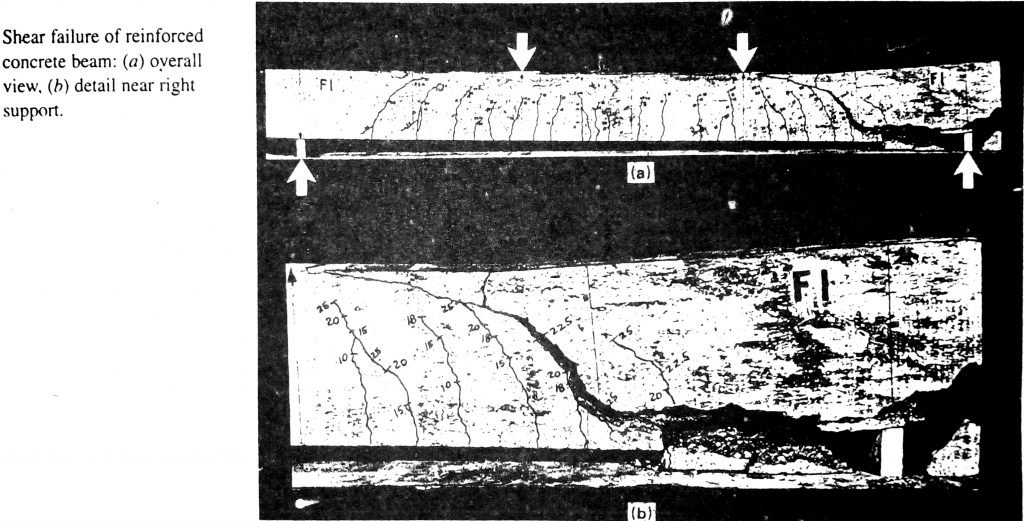
Shear failure of reinforced concrete, more properly called diagonal tension failure, is one example. Shear failure is difficult to predict accurately. In spite of many decades of experimental research and the use of highly sophisticated analytical tools, it is not yet fully understood. Furthermore, if a beam without properly designed shear reinforcement is overloaded to failure, Shear collapse is likely to occur suddenly, with no advance warning of distress. This is in strong contrast with the nature of flexural failure. For typically under reinforced beams, flexural failure is initiated by gradual yielding of the tension steel, accompanied by obvious cracking of the concrete and large defalcations, giving ample warning and providing the opportunity to take corrective measures. Because of these differences in behavior, reinforced concrete beams are generally provided with special shear reinforcement to ensure that flexure would occur before shear failure if the member should be severely overloaded.
Figure below shows a shear-critical beam tested under third point loading. With no shear reinforcement provided, the member failed immediately upon formation of the critical crack in the high-shear region near the right support.
It is important to realize that shear analysis and design are not really concerned with shear as such. The real concern is with diagonal tension stress, resulting from the combination of shear stress and longitudinal flexural stress. Most of this chapter deals with analysis and design for diagonal tension, and it provides background for understanding and using the shear provisions of the 2002 ACI code. Members without web reinforcement are studied first to establish the location and orientation of cracks and the diagonal cracking load. Methods are then developed for the design of shear reinforcement according to the present ACI code, both in ordinary beams and in special types of members, such as deep beams.
Alternative Methods for Shear Design
Over the years, alternative methods of shear design have been proposed, based on variable angle truss models and diagonal compression field theory. These approaches will be reviewed briefly later in this chapter, with one such approach, the modified compression field theory, presented in detail.
Finally, there are some circumstances in which consideration of direct is appropriate. One example is in the design of composite members combining recast beams with a cast-in-place top slab. Horizontal shear stresses on the interface between components are important. The shear friction theory, useful in this and design of beams for diagonal tension.